|
|

aerodynamic
resistance and the use of aerodynamic coefficientsA streamlined shape has much less drag than a
non-streamlined shape. Whatever drag exists for a streamlined shape is
composed primarily of skin-friction drag with the pressure drag being very
small. The increase in skin-friction drag occurs because the streamlined
body has more area exposed to the airflow and thus has a greater area over
which the boundary layer may act. A streamlined shape also experiences
almost no boundary-layer separation.
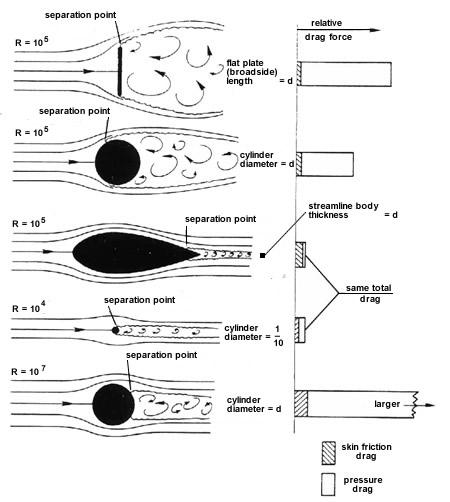
Effects of
streamlining at various Reynolds numbers.
However, the shape of a body or different airspeeds
encountered cannot explain all aerodynamic results relating to the amount
of drag. A better measure of performance is needed. This measure is the
non-dimensional drag coefficient.
From everyday experience, consider the factors that
determine the aerodynamic resistance on a body. If one places his hand
perpendicular to the airflow outside a car window that is travelling at 20
kilometres per hour (about 12 miles per hour), little resistance is felt,
but if one speeds along at 100 kilometres per hour (about 62 miles per
hour), the force felt is considerable. Velocity is one factor that
determines resistance. In fact, considering the flow problems of subsonic
flight, the resistance depends directly on (velocity) multiplied by
(velocity) or (velocity)2. Although a body moving at a velocity
of 100 kilometres per hour has a velocity that is five times that of a
body moving at 20 kilometres per hour, the aerodynamic resistance is about
25 times as great at the higher velocity.
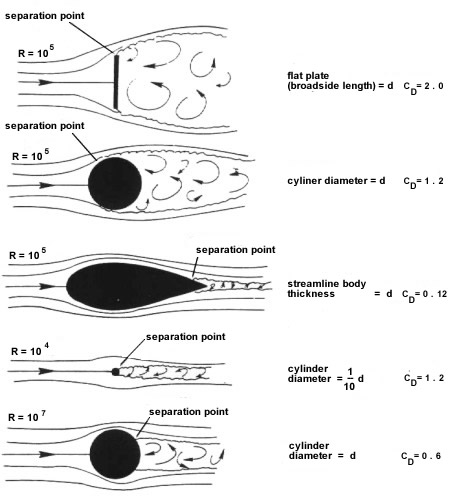
Drag coefficients of various bodies.
If one walks along a beach, there is little aerodynamic
resistance. But try to wade in the water at the same speed. It is
considerably more difficult, if not impossible. The density of water is
much greater than the density of air. Density of the fluid is
another determining factor in the resistance felt by a body.
One more experiment: hold a small piece of cardboard up
against a stiff wind. Little resistance is experienced. Now hold a much
larger but similarly shaped sheet of cardboard up against the same stiff
wind. A considerable resistance is felt. Area (or length multiplied
by length) exposed to the airflow is another determining factor of
resistance.
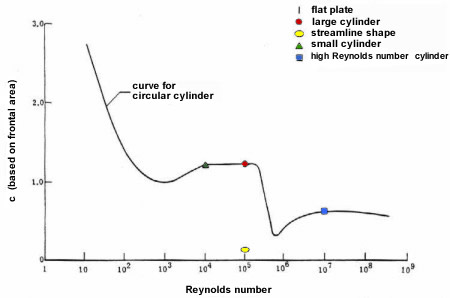
Drag
coefficients as function of Reynolds number.
We can now state that, in the flow of real
fluidairabout a body, the aerodynamic resistance depends on the size,
shape, and attitude of the body (its direction with respect to the
airflowangle of attack); the properties of the fluid, e.g., its density
and pressure; and the relative velocity between the body and the fluid
(air). To illustrate, consider the lift force, defined as the aerodynamic
reaction perpendicular to the direction of the airflow. Lift depends on
size, shape, attitude, fluid properties, and velocity. For an ideal fluid,
the fluid properties (except for density) do not influence the lift force.
For a real fluid, however, viscosity, elasticity (the reciprocal of
compressibility), and turbulent properties are also important. In addition
to the shape and attitude of the body, the surface roughness has an effect
on the force. Thus,
|
r„ |
density of the fluid |
|
V„ |
velocity of the fluid |
|
S |
body frontal area (surface area) |
|
l (or D) |
body length |
|
a |
attitude of body (angle of attack) |
|
µ |
coefficient of viscosity |
|
a„ |
speed of sound of fluid |
For a wing, S is usually taken to be the planform area (chord length
times wing span for a rectangular wing).
It has previously been shown that the quantity r„
V„ D/µ is the Reynolds number or R. Also,
that
a„/V„
is defined to be the Mach number or M. The Reynolds
number is the dimensionless quantity associated with the fluid viscosity
whereas the Mach number is associated with the fluid compressibility.
Surface roughness influences the transition from a laminar to a turbulent
flow. Air turbulence represents the degree of the wake formed past the
separation points. Furthermore, the effects of attitude and shape of a
body are lumped together into the factor called K. Then,
|
Lift = r„
x V„2 x S x K |
(2)
|
The dynamic pressure of airflow was previously defined
as 1/2 pV2 so if a value of 1/2 is included in equation
(1) and the value of K is doubled to keep the equation the same, 2K may be
replaced by CL. Finally,
Lift = CL x ½
r„ x V„2 x S
|
Lift = CL x
½ r„ x V„2 x
S |
(3)
|
Equation (3) is the fundamental lift formula for usual
aircraft flight. CL is known as the coefficient of lift. The
equation states simply that aerodynamic lift is determined by a
coefficient of lift times the free-stream dynamic pressure r„
times the characteristic body area S.
It is very important to realize that the lift
coefficient CL depends upon the Reynolds number, Mach number,
surface roughness, air turbulence, attitude, and body shape. It is not a
constant. CL is generally found by wind tunnel or flight
experiments by measuring lift and the free-stream conditions and knowing
the body dimensions. Thus,
The aerodynamic drag is the aerodynamic resistance
parallel to the free-stream direction (the direction of the airflow).
One obtains analogous equations to equations (3) and (4), namely,
where CD is the drag coefficient, dependent on the
previously enumerated parameters.
The moment acting on a body is a measure of the
body's tendency to turn about its centre of gravity. This moment
represents the resultant aerodynamic force times a moment distance. A
similar derivation may be applied to the moment equation as used for the
lift and drag equations such that,
or
Cm is the coefficient of moment and an
additional characteristic length l is necessary for it to be
dimensionally correct. To reiterate, CL, CD, and Cm
are dependent on the Reynolds number, Mach number surface
roughness, air turbulence, attitude, and body shape.
The point on an airfoil where the boundary layer
changes from laminar to turbulent is called the transition point. The
Reynolds numbers around that point are called the
critical Reynolds
numbers.
|
 |
