Alexander McKee begins his fascinating book, Great Mysteries of Aviation, with the observation that the most puzzling mystery in the history of aviation is why it took so long for humankind to learn to fly. With so much intellectual and physical energy devoted to a single problem for so long, one might have expected someone to stumble on the secret, if only by accident, long ago. What was the obstacle? The problem is that the physical principles that lie at the foundation of flight are counterintuitive; indeed, the mechanics of flight were ultimately revealed after some  fancy manipulation of the physics and mathematics created by Sir Isaac Newton in the late 1600s. Not only were the theories of Aristotle, Bacon, Leonardo, and the rest all wrong, but the true principles of flight, including how birds stay aloft, were simply un-guessable and un-observable.

It took several remarkable scientists, including members of a celebrated family of scientific giants, to piece together the puzzle. For all the triumphs of Newtonian physics—from explaining the tides to predicting comets—Newton had little success in applying his methods to fluids and fluid dynamics. Along came the Bernoullis, a Swiss family among whom were some of the most important contributors to the development of mathematics and science in the seventeenth and eighteenth centuries. The two key figures in this family were Johann (1667—1 748), who made the University of Basel in Switzerland the centre of European science in its day, and his son Daniel (1700—1782). In 1725, Daniel accepted an appointment in St. Petersburg, Russia, where he stayed for eight years and did some of his most important work. He managed to take a friend with him: the great mathematician Leonhard Euler, who had been a student of Johann Bernoulli back in Basel.

In 1734, Daniel completed his famous work Hydrodynamica,  which was not published until 1738. In addition to coining the word “hydrodynamics,” Daniel laid out the basic principles of the new science, applying Newton’s basic laws to simplified cases of fluid dynamics. Out of this work came Bernoulli’s Principle (or Law), which Euler helped express as a mathematical equation known as Bernoulli’s Equation. What Bernoulli found boiled down to this: when a fluid is moving—through a pipe or conduit, or simply over any surface—it exerts pressure in all directions: against anything that is in the way of its flow, as well as against any surface it touches. For example, as water flows through a garden hose, you can feel the pressure of the water against the inner wall of the hose if you try to squeeze the hose. Now, if the fluid is non-compressible (meaning it can’t he squeezed into a smaller volume, which is true of water, in most ordinary circumstances), and if there is no change in the amount of fluid flowing (meaning nothing is leaking out or coming in), then the faster the fluid is flowing, the lower its pressure against the surface it’s flowing over will be.

That means that when you pinch the garden hose slightly in the middle and the water keeps coming out of the end at the same rate, then the water must be travelling through the pinched portion a little faster (since the same amount of water is passing through that section of the hose as before). Our intuition is that faster water exerts greater pressure (and it does, but only in the direction of the flow), but the pressure of the faster water against the wall of the hose (which is perpendicular to the direction of the flow) is less—a total surprise. Euler gave Bernoulli’s work mathematical form (with the help of the work of French mathematician Jean le Rond d’Alembert), and Johann, Daniel’s father, made it intuitively palatable in his 1743 work, Hydraulica (which he tried to pass off as having been written in 1728).

Now, as to flying: if a sleek, symmetrical wing is in an air flow so that air is passing over it and under it, the flow can be considered non-compressible and a closed system—a few feet back (if the wing is sleek enough and the wind is not too strong), one wouldn’t even know the air took a little detour around the wing. As the air flows over the wing’s surface, it too exerts pressure in two directions—in the direction of its flow (that’s the force of the wind) and perpendicular to its flow against the surface of the wing. But since the air has to travel a greater distance to flow around the wing, it speeds up, and by Bernoulli’s Principle it exerts less pressure on the surface of the wing.

Since the wing is symmetrical (a teardrop shape in cross-section), the reduced pressure is the same both above and below. Now what happens if we slice the wing in half, so that the lower surface is straight (and the air flows across it in a straight line), hut the upper surface is curved (and the air speeds up only when flowing over that surface)? The pressure of the air on the upper surface drops, making the pressure of the air on the underside greater. The difference between the pressure upward on the underside of the wing and the force downward on the top surface is called “lift”; the curve of the top surface of a wing over its under surface is called its “camber.”

After centuries of believing the very reasonable notion that, like ships floating on the ocean, birds flew in a sea of air, and that a wing (of a bird or of a successful aircraft) would have a cross-section that, like a boat, would be curved on the bottom and flat on top, the exact opposite turned out to he the case. Flight is made possible by the lift created by the pressure difference resulting from air flowing over a wing with camber, and that’s the secret of flight.

Bernoulli's principle thus says that a rise (fall) in pressure in a flowing fluid must always be accompanied by a decrease (increase) in the speed, and conversely, if an increase (decrease) in , the speed of the fluid results in a decrease (increase) in the pressure. This is at the heart of a number of everyday phenomena. As a very trivial example, Bernouilli's principle is responsible for the fact that a shower curtain gets "sucked inwards'' when the water is first turned on. What happens is that the increased water/air velocity inside the curtain (relative to the still air on the other side) causes a pressure drop. The pressure difference between the outside and inside causes a net force on the shower curtain which sucks it inward. A more useful example is provided by the functioning of a perfume bottle: squeezing the bulb over the fluid creates a low pressure area due to the higher speed of the air, which subsequently draws the fluid up. This is illustrated in the following figure.

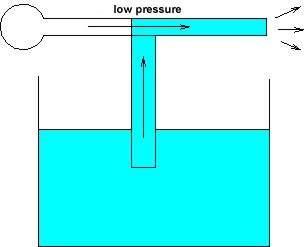
Action of a spray atomizer

Bernouilli's principle also tells us why windows tend to explode, rather than implode in hurricanes: the very high speed of the air just outside the window causes the pressure just outside to be much less than the pressure inside, where the air is still. The difference in force pushes the windows outward, and hence explode. If you know that a hurricane is coming it is therefore better to open as many windows as possible, to equalize the pressure inside and out.

Another example of Bernoulli's principle at work is in the lift of aircraft wings and the motion of ``curve balls'' in baseball. In both cases the design is such as to create a speed differential of the flowing air past the object on the top and the bottom - for aircraft wings this comes from the movement of the flaps, and for the baseball it is the presence of ridges. Such a speed differential leads to a pressure difference between the top and bottom of the object, resulting in a net force being exerted, either upwards or downwards. This is illustrated in the following figure.

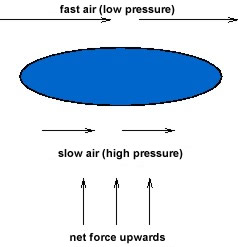
Lift of an aircraft wing