
a physical
description of lift
extracts from
www.rmcs.cranfield.ac.uk
There are several
"definitions" of lift that may be found by searching through the relevant
literature but only one that is really fundamentally correct. Sometimes the
lift is defined as "the force that is required to support the weight of the
aircraft in flight". On first inspection this seems to make sense and indeed
it is true in the case of steady level flight. However, it is otherwise
patently not the case, e.g. when the aircraft is performing a manoeuvre. The
only truly correct definition which works for all possible flight conditions
is:
the component of aerodynamic
force generated on the aircraft which acts perpendicular to the instantaneous
flight direction.
This means that the lift is
inclined backwards in a climb, forwards in a dive and inwards in the case of a
banked turn (Fig 1).
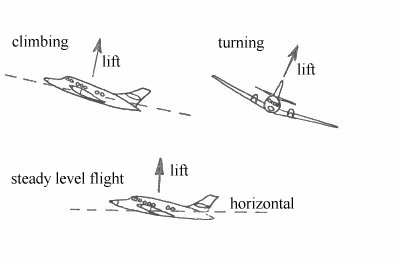
Lift Force acting on an Aircraft
The overall force may be attributed to two
natural phenomena:
-
- the variable static pressure distribution,
acting perpendicular to the surface.
-
- the variable shear stress distribution,
acting tangential to the surface.
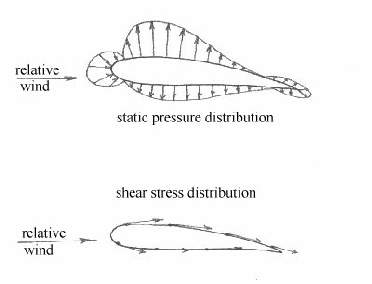
Static Pressure & Shear Stress Distributions
It is clear that, as far
as lift is concerned, the shear stress is secondary and contributes mainly
to the drag force. The lift force itself is primarily due to the pressure
distribution imbalance over the upper and lower surfaces. In particular,
the production of a lower net pressure across the surface relative to the
lower surface will produce an upwards lift force. It is therefore often
convenient to only deal with the pressure forces when discussing the
physical origin of the lift force. This will form the basis of all the
following reasoning on the subject.
Aerofoil Section
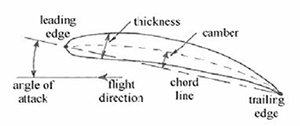
Subsonic Aerofoil Section Geometry
Most of this discussion on
lift will be centred on typical subsonic aerofoil sections. and it is
therefore worthwhile reviewing their basic geometry. This is shown above, with
the camber and thickness exaggerated to aid clarity (more typically around 3%
and 12% of the chord length respectively). It is worth noting that any shape
may be made to produce lift , provided it is given either camber or inclined
to the flow direction (i.e. given an angle of attack). It is the need to
optimise the lift/drag ratio which leads to the use of the classical
streamlined aerofoil sections.
Magnus Effect
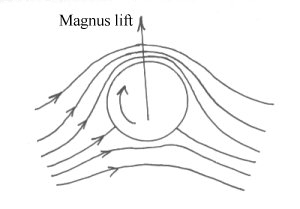
From the discussion on the
circulation theory of lift it should be apparent that any rotating object
placed in a moving air stream will produce circulation and hence aerodynamic
lift. This is then known as the magnus lift and produces many familiar
effects such as the top/back/side spin on tennis balls and the hook/slice of a
golf ball.
Normal Force & Lift
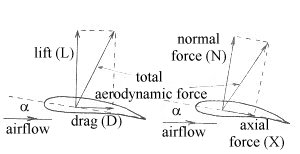
Lift/Drag and Normal Force/Axial Force
While it is mostly convenient
to deal with aerodynamic lift, there are occasions when it is best to make use
of a different resolution of the aerodynamic force in which it is broken down
into normal force and axial force instead of lift and drag. It
should be recalled that lift and drag are the resolved components relative to
the airflow direction (lift is perpendicular to it, drag is parallel to it).
If the total force is resolved relative to the chord line of the wing instead,
then the components are known as the normal force and axial force.
The vector sum of the two components will always be the same, of course, i.e.
equal to the total aerodynamic force.
A pair of general trigonometric relationships
between the components may easily be derived:
L = N cosα - X sinα
D = N sinα + X cosα
Clearly, in cases where the
chord line and airflow are coincident (i.e. when α = 0), then L = N and D = X.
The use of N instead of L is especially useful when it comes to dealing with
the stability and control aspects of an aircraft.
Lift Curves of Finite
Wings
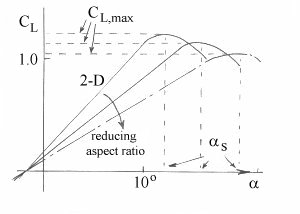
Aspect Ratio Effect Upon Lift Curve Slope
The lift curve slope (a)
reduces as aspect ratio reduces, as shown in Fig 1. This is due to the
downwash angle produced, which reduces the effective angle of attack of the
wing . A useful expression for determining the lift curve slope for an
unswept finite wing is:
-
a = ao / [(1 + 57.3
ao) / (π e A)] per degree
where:
-
ao is the 2-D lift
curve slope,
-
e is the span effectiveness
(Oswald) factor, and
-
A is the wing aspect ratio.
The aspect ratio is the
primary factor as both e and ao are reasonably similar for most
conventional wing designs. The 2-D lift curve slope is obtained from specific
aerofoil data and is theoretically equal to 2π per radian (or 0.1097 per
degree) for a thin aerofoil but is more typically around 0.105 per degree. The
curves are also slightly affected by Reynolds number (Re) and the application
of high lift devices.
Example
Calculate the lift curve slope
for a NACA 23012 wing of 2-D lift curve slope = 0.106 per degree, aspect ratio
= 10, Re = 5 x 106 and span effectiveness factor = 0.95.
Solution:
a = ao / [(1 + 57.3
ao) / (π e A)] = 0.088 per degree
Wing Sweep and Mach Number
Effects
Both wing sweep (Λ¼)
and Mach number (M) affect the lift curve slope. A useful expression for its
derivation (ref Howe) in this instance is given below:
a = 2π / [(0.32 + (0.16 A /
cos Λ¼)) (1 - (M cosΛ¼)2)½] per
radian
Note that the Oswald
efficiency factor and 2-D lift curve slope terms are no longer present as it
is the sweep, aspect ratio and Mach number which are the dominant factors.
Example
Calculate the lift curve slope
for a wing of aspect ratio = 10, quarter-chord sweepback angle = 33o
and M = 0.82.
Solution:
a = 2π / [(0.32 + (0.16 A / cos Λ¼)) (1 - (M cosΛ¼)2)½]
= 2π / 1.617 = 3.88 per radian or 0.068 per degree
Alternative Lift Theory - Newton's 3rd Law of Motion
An alternative explanation
which is sometimes given in textbooks on flight mechanics uses Newton's laws
of motion as a basis. The reasoning is that the wing deflects the air
downwards so that the wing imparts a downward component to it. To do so, the
wing must be providing a downwards force on the air (Newton's 1st Law). Then
from Newton's 3rd Law, the air must be providing an equal and opposite
reaction force on the wing.
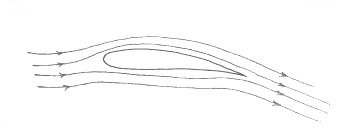
Downwards Air Deflection over a Lifting Wing
This explanation is certainly
better than the standard but it could be argued that this is the effect
of lift rather than the cause of it. There is no doubt that air is
deflected downwards and indeed that a considerable amount of air movement is
required in order to provide the requisite amount of wing lift. It could,
however, be the pressure distribution which is pushing the wing up and that
this is really the action which is taking place. The reaction to
this would then be for the wing to push the air down, with a sufficient
momentum change to balance out the lift produced. This would mean that the
original argument is probably the "wrong way around"!
Drag Components - Trailing Vortex Drag
Any lift-producing surface,
such as an aircraft wing, will inevitably produce compensating wing-tip
vortices. This is due to the presence of a relatively low pressure on the wing
upper surface compared with the lower surface. This pressure difference must
equalise at the wing tips and the net result is a movement of airflow along
the span of the wing, from the high pressure region to the low pressure
region. The airflow therefore tends to move outwards towards the tip on the
lower surface and inwards to the centre of the aircraft along the upper
surface. When combined with the airstream this produces a pair of
contra-rotating vortices at the wing tips.
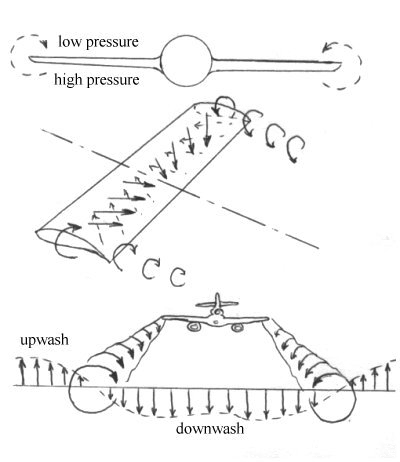
Trailing Vortices Producing Downwash
The vortices force the air to
move downwards across the whole span of the wing, known as downwash.
Outboard of the wing tips, the air experiences an upwash flow, which
explains why flocks of birds tend to fly in a V-formation.
The downwash component
produces a drag component known as either trailing vortex drag or lift-induced drag, as shown below. The downwash component may be added to
the original airstream velocity vector to produce a revised airflow component
which is now at a lower angle of attack than previously. Since lift is
proportional to angle of attack this means that the overall lift is reduced.
It also means that the lift vector is tilted rearwards as it is defined as
being perpendicular to the airstream vector. If the revised lift term is now
split back into its original directional components it is clear that there
must be a drag term (Di) present.
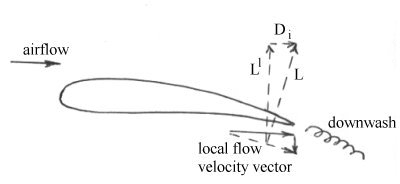
Downwash Effect
The aspect ratio is the primary factor as both
e and ao are reasonably similar for most conventional wing designs.
The 2-D lift curve slope is obtained from specific aerofoil data and is
theoretically equal to 2π per radian (or 0.1097 per degree) for a thin
aerofoil but is more typically around 0.105 per degree. The curves are also
slightly affected by Reynolds number (Re) and the application of high lift
devices.
Example
Calculate the lift curve slope for a NACA
23012 wing of 2-D lift curve slope = 0.106 per degree, aspect ratio = 10, Re =
5 x 106 and span effectiveness factor = 0.95.
Solution:
a = ao / [(1 + 57.3 ao)
/ (π e A)] = 0.088 per degree
Wing Sweep and Mach Number Effects
Both wing sweep (Λ¼) and Mach
number (M) affect the lift curve slope. A useful expression for its derivation
(ref Howe) in this instance is given below:
a = 2π / [(0.32 + (0.16 A / cos
Λ¼)) (1 - (M cosΛ¼)2)½] per radian
Note that the Oswald efficiency factor and 2-D
lift curve slope terms are no longer present as it is the sweep, aspect ratio
and Mach number which are the dominant factors.
Example
Calculate the lift curve slope for a wing of
aspect ratio = 10, quarter-chord sweepback angle = 33o and M =
0.82.
Solution:
a = 2π / [(0.32 + (0.16 A / cos Λ¼)) (1 - (M cosΛ¼)2)½]
= 2π / 1.617 = 3.88 per radian or 0.068 per degree
Correct
Physical Explanation of Origin of Lift
A more fundamentally correct
explanation for the origin of aerodynamic lift may be found by making use of
the conservation laws of physics, namely mass flow (continuity) and energy
(Euler or Bernoulli).
Consider the 2-D stream tubes
A and B shown below - these are originally of the same width when well
upstream of the aerofoil and out of its influence. The common streamline
between them is aligned with the leading edge stagnation point so acts to
divide the airflow over the top and bottom surfaces. The stream tube A
encounters the upper portion of the aerofoil and is "squashed" through what is
effectively a smaller area. Stream tube B is squashed less resulting in a
larger stream tube width relative to A. From continuity (dm/dt = ρ A V) this
must mean that the velocity in A must be greater than in B.
Either Euler's (dp = - ρ VdV)
or Bernoulli's (p + ½ ρ V2 = constant) theorems may now be applied
to show that pA must be less than pB. This results in
the pressure distribution shown below. It can be seen that the majority of
lift is due to the low pressure (suction) acting over the upper surface,
particularly over the front 20% to 30%, where the flow accelerations are at
their most severe.
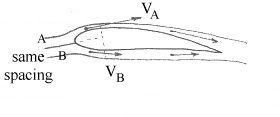
Changes in Stream Tube Spacing
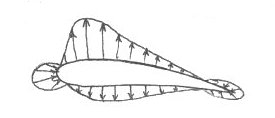
Resultant Pressure Distribution
t) and the table puts an equal
and opposite force on the object to hold it up. In order to generate lift a
wing must do something to the air. What the wing does to the air is the action
while lift is the reaction.
|
