One of the most commonly stated definitions of the Manoeuvring speed, is the speed at which the pilot can use full control deflections without over-stressing the airplane. The above definition is reasonably correct, although it should be limited to "full nose up control deflections" without over-stressing the airplane. This definition however does not give us the insight we need to create an equation which will give us the Manoeuvring speed of our airplane. To do that we need to consider why there is a speed below which it is impossible to overstress the airplane.

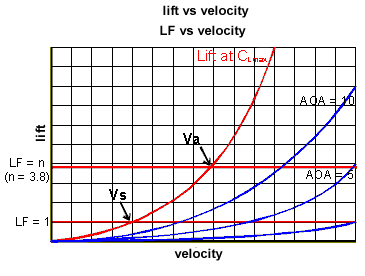
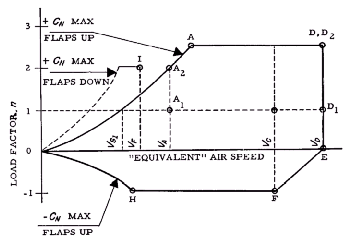
In the diagram to the right the maximum lift the wing can produce is shown in red. The LF=1 line shows the stall speed, as we learned in the previous section. The LF=n (n=3.8) line shows the minimum speed at which the wing can produce lift equal to the design Load Factor. This is the definition of Manoeuvring speed we need.

The Manoeuvring Speed is the minimum speed at which the wing can produce lift equal to the design load limit. Below this speed the wing can not produce enough lift to overstress the aircraft, no matter what angle of attack is used.

The design load limit is specified by the FAA for USA designed aircraft and Transport Canada for Canadian designed aircraft. In Module 5 we will explore all the aircraft limitations required by law.

For most normal aircraft the design load limit is 3.8g.

Manoeuvring Speed Formula

It is obvious that the Manoeuvring speed is closely related to the stall speed. We could in fact create a formula for Manoeuvring speed which is identical to the stall speed equation except with lift equal to n times the weight:

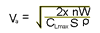
This equation is virtually identical to the Stall speed equation:

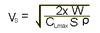
The only difference is that the Manoeuvring speed depends upon the square root of nW not just the square root of W. Therefore we can express Va in terms of Vs as:
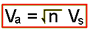