The performance of an aircraft in the hands of a competent pilot – at a given altitude – results from the sum of power and attitude. Power provides thrust and consequently forward acceleration, lift, drag and radius of turn. Attitude is the angle of the longitudinal axis with the horizon (often called the 'pitch' which also has another meaning associated with propellers) plus the angle of attack and the angle of bank. Attitude dictates the direction and dimension of the lift, thrust and drag vectors and consequently converts power into velocities and accelerations in the three planes. There is a third factor – energy management – which is an art that supplements attitude plus power to produce maximum aircraft performance. The epitome of such an art is demonstrated by air-show pilots who produce extraordinary performances from otherwise relatively mundane aeroplanes.

Cruise performance

When an aircraft is in cruise mode, i.e. flying from point A to point B, the pilot has several options for cruise speed. One choice might be to get there as soon as possible, in which case she/he would operate the engine at the maximum continuous power allowed by the engine designer. The recommended maximum continuous power is usually around 75% of the rated power of the engine and provides performance cruise. Another choice might be to get there using as little fuel as possible, but in a reasonable time, in which case the pilot might choose a 55% power setting to provide the economy cruise airspeed. Or the pilot might choose any power setting, in the usual engine design range, between 55% and 75%.

(Rated power is the brake horsepower delivered at the propeller shaft of a direct drive engine, operating at maximum design rpm and best power fuel/air mixture, in standard sea level air density conditions. An engine is only operated at its rated capacity for short periods during flight. Rated power for small aero-engines is usually expressed as brake horsepower rather than the SI unit of kilowatts.

The power required curve

In level flight at constant speed the power is only required to balance drag. Power is the rate of doing work so power (watts) is force (newtons) × distance (metres) / time (seconds). Distance/time is velocity so power required is drag force (N) × velocity (v)
Thus if we use the expression for total drag in section 1.6 and multiply it by v we get:-

  Power required for level flight = C_D × ½rV³ × S watts  [note  V³  ]

 The total drag curve in the section 1.6 diagram can be converted into a 'power required' curve – usually called the power curve – if you know the total drag at each airspeed between the minimum controllable speed and the maximum level flight speed. It will be a different curve to that for total drag, because the power required is proportional to velocity cubed rather than velocity squared: which means that if speed is doubled drag is increased four-fold but power must be increased eight times. Which indicates why increasing power output from say 75% to full rated power (100%) while holding level flight doesn't provide a corresponding increase in airspeed – see below.

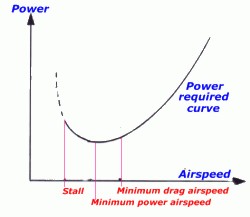
The diagram above is a typical level flight power curve for a light aeroplane, the part of the curve to the left of the minimum power airspeed is known as the back of the power curve where the slower you want to fly the more power is needed, because of the induced drag at the high angles of attack of low speeds. The lowest possible speed for controlled flight is the stall speed, which we will discuss in the 'Airspeed and air properties' module. Two cruise speeds are indicated – the speed associated with minimum power and the speed associated with minimum drag. The former is known as Vbe and the latter as Vbr.

Power available

   The engine provides power to the propeller. The propellers used in most light aircraft have a maximum efficiency factor, in the conversion of engine power to thrust power, of no more than 80%. (Thrust power = thrust × forward velocity). The pitch of the blades, the speed of rotation of the propeller and the forward velocity of the aircraft all establish the angle of attack of the blades and the thrust delivered. The in-flight pitch of light aircraft propeller blades is usually fixed so that the maximum efficiency will occur at one combination of rpm and forward velocity; this is usually in the mid-range between best rate of climb and the performance cruise airspeeds. Propeller blades are sometimes pitched to give the maximum 80% efficiency near the best rate of climb speed, or pitched for best efficiency at the performance cruise airspeed. The former is a climb prop and the latter a cruise prop. The efficiency of all types falls off either side of the maximum; one with too high pitch angle may have a very poor take-off performance; one with too low pitch may allow the engine to overspeed at any time.

Speed, power and altitude

 At sea level an aero engine will deliver its rated power – provided it is in near perfect ex-factory condition, properly warmed up and using fuel in appropriate condition. However as air density decreases with altitude, and an engine's performance is dependent on the weight of the charge delivered to the cylinders, then the full throttle power of a non-supercharged four-stroke engine will decrease with height, so that at about 6000 – 7000 feet the maximum power available at full throttle may drop below 75% of rated power. At 12 000 feet full throttle power may be less than 55% rated power. Thus as altitude increases the range of cruise power airspeeds decreases. For best engine performance select a cruise altitude where the throttle is fully open and the engine is delivering 65% – 75% power.

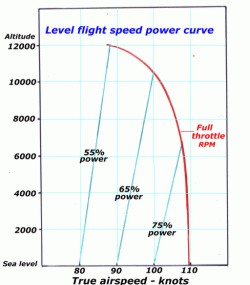
A couple of points to note in the speed-power diagram above: firstly as air density, and consequently drag, reduces with height then airspeed from a particular power level will increase with height; e.g. the airspeed attained with 65% power at sea level is 90 knots increasing to 100 knots at 10 000 feet. Secondly at sea level an increase in power from 75% to 100% only results in an increase in airspeed from 100 to 110 knots. This is the norm with most light aircraft – that last 33% power increase to rated power only provides a 10% increase in airspeed.

Power required vs power available

In the diagram below, power available curves have been added to the power required curve. The upper curve indicates the rated power i.e. the full throttle engine power delivered to the propeller over the range of level flight speeds at sea level. The second curve, maximum available thrust power, is that engine power converted by the propeller after allowing for 80% maximum propeller efficiency. The third curve is the propeller thrust power available with the engine throttled back to 75% power at sea level, or, if flying at an altitude such that full throttle opening will only deliver 75% of rated power. The intersection of those power available curves with the power required curve indicates the maximum cruise speed in each condition.

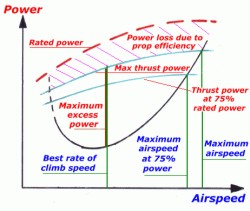
The region between the green maximum available thrust power curve and the power required curve indicates the excess power available at various cruise speeds, and this excess power is available for various manoeuvres. The simplest use would be a straight unaccelerated climb, in which case the maximum rate of climb would be achieved at the airspeed where the two curves are furthest apart; this airspeed is Vy; best rate of climb speed. It can be seen that the Vy is about the same airspeed as the speed for minimum drag – Vbr – shown in the powered required curve.

It is important to remember that the rate of climb will decrease at any speed either side of Vy because the power available for climb decreases. The rate of climb (metres/second) = excess power available (watts)/aircraft weight (newtons).

Forces in a climb

It was said above that in cruise the difference between the current power requirement and power available – the excess power – can be used to accelerate the aircraft or climb, to accelerate and climb, or perform any manoeuvre which requires additional power. For instance if the pilot has potential power available and opens the throttle the thrust will exceed drag and the pilot can utilise that extra thrust to accelerate to a higher speed while maintaining level flight. Alternatively the pilot can opt to maintain the existing speed but use the extra thrust to climb to a higher altitude. The rate of climb (altitude gained per minute) depends on the amount of available power utilised for climbing, which depends in part on the airspeed chosen for the climb. There are other choices than Vy available for the climb speed, for example Vx the best angle of climb speed or a combination enroute cruise/climb speed.

If an aircraft is maintained in a continuous full-throttle climb at the best rate of climb airspeed the rate of climb will be highest at sea level and decrease with altitude as engine power decreases. It will eventually arrive at an altitude where the excess power available for climb reaches zero. All the available power is required to balance the drag in level flight, and there will be only one airspeed at which level flight can be maintained and, below which, the aircraft will stall. This altitude is the aircraft's absolute ceiling. However unless trying for an altitude record there is no point in attempting to climb to the absolute ceiling so the aircraft's service ceiling should appear in the aircraft's performance specification. The service ceiling is the altitude at which the rate of climb falls below 100 feet per minute, such being considered the minimum useful rate of climb.

This diagram of forces in the climb and the subsequent expressions, have been simplified, aligning the angle of climb with the line of thrust. In fact the line of thrust will usually be 4° to 10° greater than the climb angle. The climb angle is the angle the flight path subtends with the horizon.

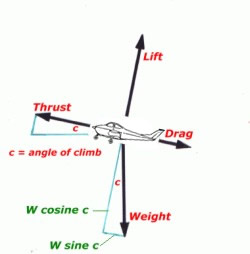
The relationships in the triangle of forces shown is:-
Lift = weight × cosine c
Thrust = drag + (weight × sine c)

In a constant climb the forces are again in equilibrium but now thrust plus lift = drag plus weight.

Probably the most surprising thing about the triangle of forces in a straight climb is that lift is less than weight! For example let's put the Jabiru into a 10° climb with weight = 4000 newtons. (There is an abridged trig. table at the end of this page.)

then       Lift = W cos c = 4000 × 0.985 = 3940 newtons

It is power that provides a continuous rate of climb, but momentum may also be used as a temporary energy exchange expedient, refer section 1.11 below. It is evident from the above that in a steady climb the rate of climb (and descent) is controlled with power and the airspeed and angle of climb is controlled with the attitude. This is somewhat of a simplification as the pilot employs both power and attitude in unison to achieve a particular angle and rate of climb or descent.

A very important consideration, particularly when manoeuvring at low level at normal speeds, is that the steeper the climb angle the more thrust is required to counter weight. For example if you pulled the Jabiru up into a 30° climb the thrust required = drag + weight × sine 30° and sine 30° = 0.5 so the engine has to provide sufficient thrust to pull up half the weight plus overcome the increased drag due to the increased aoa in the climb. Clearly not possible so the airspeed will fall off very rapidly and will lead to a dangerous situation if the pilot is slow in getting the nose down to an achievable attitude.

Forces in a descent

If an aircraft is cruising at, for instance, the maximum 75% power speed and the pilot reduces the throttle to 65% power, the drag now exceeds thrust and the pilot has two options – maintain height allowing the excess drag to slow the aircraft to the level flight speed appropriate to 65% power or maintain the existing speed and allow the aircraft to enter a steady descent or sink. The rate of descent (altitude lost per minute) depends on the difference between the 75% power required for level flight at that airspeed and the 65% power utilised. This sink rate will remain constant as long as the thrust plus weight, which are together acting in a forward direction, are exactly balanced by the lift plus drag, which are together acting in a rearward direction. At a constant airspeed the sink rate, and the angle of descent, will vary if thrust is varied.

If the pilot now pushed forward on the control column to a steeper angle of descent, while maintaining the same throttle opening, the thrust plus weight resultant vector becomes greater, the aircraft accelerates with consequent increase in thrust power and the acceleration continues until the forces are again in equilibrium. Actually it is difficult to hold a stable aircraft in such a fixed angle "power dive" as the aircraft will be wanting to climb – but an unstable aircraft might be wanting to 'tuck under' i.e. increase the angle of dive, even past the vertical.

When the pilot closes the throttle completely, there is no thrust, the aircraft enters a gliding descent and the forces are then as shown in the diagram on the left. In the case of a constant rate descent the weight is exactly balanced by the resultant force of lift and drag. From the dashed parallelogram of forces shown it can be seen that the tangent of the angle of glide equals drag/lift.

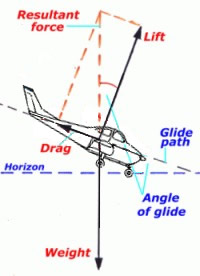
For example assuming a glide angle of 10°, from the table below the tangent of 10° is 0.176, so the ratio of drag/lift in this case is then 1 : 5.7
Conversely we can say that the angle of glide is dependent on the ratio of lift/drag and the higher that ratio is then the smaller the glide angle and consequently the further the aircraft will glide from a given height.

e.g. calculating the optimum glide angle for an aircraft with a L/D of 12 :1:-
Drag/lift equals 1/12 thus tangent = 0.08 and, from the table below, the glide angle = 5°.

Although there is no thrust associated with the power-off glide the power required curve in section 1.7 above is still relevant. The minimum drag airspeed shown in that diagram is more or less the airspeed for best glide angle – Vbg – and the speed for minimum power is more or less the airspeed for minimum rate of descent in a glide – Vmd.

Turning forces

Load factors

In aviation usage "g" denotes the force due to gravity. When an aircraft is airborne at a constant velocity and altitude the load on the aircraft wings is the aircraft's mass and that load is expressed as being equivalent to '1g'. Similarly when the aircraft is parked on the ground the load on the aircraft wheels [its weight] is a 1g load.

Any time an aircraft's velocity is changed there are positive or negative accelerative forces applied to the aircraft and its occupants. The resultant "load factor" is normally measured in terms of "g" load which is the ratio of the forces experienced during the acceleration to the forces existing at 1g.

You will come across expressions such as "2g turn" or "pulled 2g"; what is being implied is that during a particular manoeuvre a radial acceleration was applied to the airframe and the load on the wings doubles – for the Jabiru a 2g load = 400 kg × 20 m/s² = 8000 newtons. The occupants will also feel they weigh twice as much. This is 'radial g', or centripetal force and it applies whether the aircraft is changing direction in the horizontal plane, the vertical plane or anything between.

You may also come across mention of "negative g". It is conventional to describe g as positive when the loading on the wing is in the normal direction. When the load direction is reversed it is described as negative. Slight negative g can occur momentarily in severe turbulence but an aircraft experiencing a sustained 1g negative loading is flying in equilibrium, but upside down. It is also possible for some high powered aerobatic aircraft to fly an 'outside' loop, i.e. the pilot's head is on the outside of the loop rather than the inside, and the aircraft (and it's very uncomfortable occupants), will be experiencing various negative g values all the way around the manoeuvre.

The structures of the aircraft we are concerned with are required to withstand in-flight load factors not less than +4.4g to –1.8g at MTOW without any malformation – temporary or otherwise. In addition, to allow for less than optimum craftmanship, a 'design safety factor' of at least 1.5 is added thus the aircraft should normally cope with load factors of +6.6g to – 2.7g.

It should not be thought that aircraft structures are significantly weaker in the negative g direction. The normal load is +1g so with a +4.4g limit then an additional positive 3.4g load can be applied while with a –1.8g limit an additional negative load of 2.8g can be applied.

Centripetal force

When an aircraft turns, in any plane, an additional force must be continuously applied to overcome inertia, particularly its normal tendency to continue in a straight line. This is achieved by applying a force towards the centre of the curve or arc – the centripetal force – which is the product of the aircraft mass and the acceleration required. Remember that acceleration is the rate of change of velocity, either speed or direction or both. The acceleration, as you know from driving a car through an S curve, depends on the speed at which the vehicle is moving around the arc and the radius of the turn. Slow speed and a sweeping turn – very little acceleration, but high speed and holding a small radius involves high acceleration with consequent high radial g or centripetal force and difficulty in holding the turn.

The acceleration towards the centre of the turn is V²/r metres per second per second and the centripetal force required to produce the turn is m × V²/r Newtons where r is the turn radius in metres and m is the aircraft mass in kilograms. Note that we are using aircraft mass not weight.

Turn forces and bank angle

The diagram below shows the relationships between centripetal force, weight, lift and bank angle.

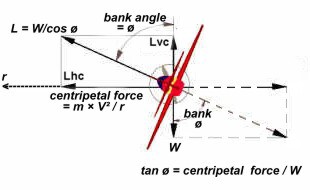
In a level turn the vertical component of the lift [L_vc] balances aircraft weight and the horizontal component of lift [L_hc] provides the centripetal force.

[Note: in a right angle triangle the tangent of an angle is the ratio of the side opposite the angle to that adjacent to the angle. Thus the tangent of the bank angle is equal to the centripetal force divided by the aircraft weight or tan ø = cf / W. (Or it can be expressed as tan ø = V² /gr ). In the diagram I have created a parallelogram of forces so that all horizontal lines represent the centripetal force or L_hc and all vertical lines represent the weight or L_vc.]
 

The centripetal force of 4000 N is provided by the horizontal component of the lift force from the wings when banked at an angle from the horizontal, the correct bank angle being dependent on the velocity and radius: think about a motorbike taking a curve in the road. During the level turn the lift force must also have a vertical component to balance the aircraft's weight, in this case also 4000 newtons. But the total required force is not 4000 + 4000 N, rather we have to find the one – and only one – bank angle where L_vc is equal to the weight and L_hc is equal to the required centripetal force.

What then will be the correct bank angle [ø] for a balanced turn? Well we can calculate it easily if you have access to trigonometrical tables, if you haven't there is a very abridged version at the end of this page.
 

Wing loading

   We know that lift = C_L × ½rV² × S = Weight
   thus W = C_L × ½rV² × S
   or    W / S = C_L × ½rV² = the wing loading

From this we can see that if wing loading increases in a constant speed manoeuvre then C_L , the angle of attack, must increase. Conversely if C_L , the angle of attack, is increased during a constant speed manoeuvre the lift, and consequently the wing loading, must increase.

It can be a little misleading when using terms such as 2g. For instance we said earlier that a lightly loaded Jabiru has a mass of 340 kg and if you do the preceding centripetal force calculation using that mass you will find that the centripetal acceleration is 10 m/s², centripetal force is 3400 N, weight is 3400 N and total lift = 4800 N, i.e. the actual wing loading is 20% less but it is still a 1.41g turn, i.e. 4800/3400 = 1.41.

Thus rather than thinking in terms of g equivalents, it may be more appropriate to consider the actual loads being applied to the aircraft structures, and the norm is to use the wing loading as the primary structural load reference. In the prior case the load on the wing structure is 5660 / 8 = 707 N/m², compared to the 500 newtons load per m² in normal cruise.

Most general aviation aircraft have a designed wing loading between 500 and 1000 N/m², ultralights between 200 and 550 N/m², in normal cruise near maximum allowed weight. Aircraft designed with higher wing loading are usually more manoeuvrable, are less affected by atmospheric turbulence, but have higher minimum speed than aircraft with lower wing loading. Wing loading is usually stated in pounds per square foot; between 11 and 22 for GA aircraft, 4 and 12 for ultralights.

Increasing the lift force in a turn

You might ask how does the Jabiru increase the lift if it maintains the same cruise speed in the level turn? Well the only value in the equation - Lift = C_L × ½rV² × S - that can then be changed is the lift coefficient, which must be increased by the pilot increasing the angle of attack. Note that increasing aoa will also increase induced drag, so that the pilot must also increase thrust to maintain the same airspeed; thus the maximum rate of turn for an aircraft will also be limited by the amount of additional power available to overcome induced drag.

Thus for a level turn the slowest possible speed and the steepest possible bank angle will provide both the smallest radius and the fastest rate of turn, but there are limitations.

If you consider an aerobatic aircraft weighing 10 000 N and making a turn in the vertical plane, i.e. the loop described earlier, and imagine that the centripetal acceleration is 2g; what will be the wing loading at various points of the turn? Actually the centripetal acceleration varies all the way around because the airspeed and radius must vary but we will ignore that and say that it is 2g all round. If the acceleration is 2g then the centripetal force must be 20 000 N all the way round.

A turn in the vertical plane differs from a horizontal turn in that, at both sides of the loop, the wings do not have to provide any lift component to counter weight, just lift for the centripetal force, so the total load at those points is 20 000 N or 2g. At the top, with the aircraft inverted, the weight is directed towards the centre of the turn and provides 10 000 N of the centripetal force and the wings need provide only 10 000 N. Thus the total load is only 10 000 N or 1g, whereas at the bottom of a continuing turn the wings provide all the centripetal force plus counter the weight, so the load there is 30 000 N or 3g.

This highlights an important point: when acceleration loads are reinforced by the acceleration of gravity, the total load can be very high.

If you have difficulty in conceiving the centripetal force loading on the wings, think about it in terms of the reaction momentum, centrifugal force which, from within the aircraft, is seen as a force pushing the vehicle and its occupants to the outside of the turn and the lift (centripetal force) is counteracting it. Centrifugal force is always expressed as g multiples.

Conserving aircraft energy

Energy available

An aircraft in straight and level flight has:

• linear momentum – m × v kg m/s

• kinetic energy [the energy of a body due to its motion] – ½mv² newton metres (or joules; one joule = 1Nm)

• gravitational potential energy – in this case the product of weight in newtons and height gained in metres

• chemical potential energy in the form of fuel in the tanks

• and air resistance that dissipates some kinetic energy as heat or atmospheric turbulence.

To simplify the text from here on we will refer to 'gravitational potential energy' as just potential energy and "chemical potential energy" as just chemical energy.
 

Because it is the accumulation of the work done to raise the aircraft 6500 feet, the potential energy is 16 times the kinetic energy, and is obviously an asset that you don't want to dissipate. It is equivalent to 2% of your fuel.

One of the skills of piloting an aircraft is in the art of managing energy for conservation and making appropriate use of momentum. Fighter pilots take the art of energy management to its limits – for survival, but so should you – the only safe place to have dissipated your potential and kinetic energy is after the aircraft touches down on the runway. The intelligent use of energy and momentum, for instance exchanging potential for kinetic, or vice versa, is a skill to be developed.

It is always wise to balance a shortage of potential energy with an excess of kinetic energy, and vice versa. For example if you don't have much height then have some extra speed up your sleeve for manoeuvring or to provide extra time for action in case of engine or wind shear problems. Or if kinetic energy is reduced by flying at lower speeds than normal make sure you have ample height or, if approaching to land, hold height for as long as possible. The only time to be "low and slow" is when you are about to land.

However during take-off it is not possible to have an excess of either potential or kinetic energy thus take-off is the most critical phase of flight, closely followed by the go-around following an aborted landing approach. Ensure that a safe climb speed is achieved as quickly as possible after becoming airborne – or commencing a go-around – and before the climb-out is actually commenced.

Kinetic energy measurement

Kinetic energy is a scalar quantity equal to ½mv² joules if the aircraft is not turning. However the velocity must be measured in relation to some frame of reference and when we discuss inflight energy management the aircraft velocity chosen is that which is relative to the air, i.e. the true airspeed. For a landborne [or about to landborne] aircraft we are generally concerned with either the work to be done to get the aircraft airborne or the [impact] energy involved in bringing the aircraft to a halt, so the velocity used is that which is relative to the ground. Groundspeed represents the horizontal component, rate of climb/descent the vertical component of that velocity.

Kinetic energy, gravitational potential energy and energy conservation are complex subjects. If you wish to go further plug "kinetic energy" "reference frame" into the Google search engine.

Momentum conversion

Let's look at momentum conversion. Take the Jabiru, weighing 4000 newtons and cruising at 97 knots – 50 m/s – and the pilot decides to reduce the cruise speed to 88 knots – 45 m/s. This could be accomplished by reducing thrust, below that needed for 88 knots, allowing drag to dissipate the excess kinetic energy then increasing power for 88 knots. However, if traffic conditions allow, the excess kinetic energy can be converted to potential energy by reducing power, but only to that needed to maintain a 88 knot cruise, and at the same time, pulling up – thus reducing airspeed but still utilising momentum – then pushing over into level flight just as the 88 knot airspeed is acquired.

If you recalculate the preceding figures doubling the initial (100 m/s) and final velocities (90 m/s) the height gained will increase fourfold to 96 metres, or about 18 feet per knot. Conversely if we halve the initial velocity to about 50 knots the height gained per knot converted is halved, to about 4 feet. Note that as mass appears in both the kinetic energy and the weight expressions, it can be ignored, thus the figures are the same for any mass.