Atmospheric pressure reflects
the average density and thus the weight of the column of air above a given
level, thus the pressure at a point on the earth's surface must be greater than
the pressure at any height above it. An increase in surface pressure denotes an
increase in mass, not thickness, of the column of air above the surface point.
Similarly a decrease in surface pressure denotes a decrease in the mass. The
gradient is the difference in pressure vertically, and horizontally.
The air throughout the column is compressed by the weight of the atmosphere
above it and thus the density of a column of air is greatest at the surface and
decreases exponentially with altitude as shown in the following graph which is a
plot of the rate of decrease in density with increase in altitude. The plot is
for dry air at mid-latitudes. ( Mid latitudes are usually accepted to be the
areas between the 30° and 60° lines while low latitudes lie between the equator
and 30° and high latitudes between 60° and the pole.) The atmosphere at
about 22 000 feet has only 50% of the sea level density, density decreases by
about 3% per 1000 feet between sea level and 18 500 feet and thereafter the
density lapse rate slows.
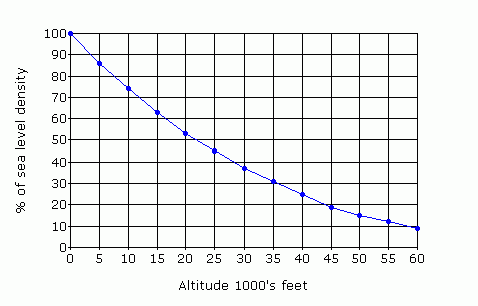
The dry air density gradient in mid-latitudes, refer table in 2.1
As the pressure decreases with
height so, in any parcel of air, the downwards pressure over the top of the
parcel must be less than the upwards pressure under the bottom: thus within the
parcel there is a vertical component of the pressure gradient force
acting upward; generally this force is balanced by the gravitational force so
the net sum of forces is zero and the parcel floats in equilibrium. This balance
of forces is called the hydrostatic balance. When the two do not quite
balance the difference is the buoyancy force which is the upward, or
downward, force exerted on a parcel of air arising from the density difference
between the parcel and the surrounding air.
Atmospheric pressure also varies horizontally, due to air mass changes
associated with the regional thickness of the atmospheric layer. The resultant
horizontal pressure gradient force, not being balanced by gravity, forces
air to move from regions of higher pressure towards regions of lower pressure
but the movement is modified by Coriolis effect. The horizontal force is about
1/15 000 of the vertical component.
(Advection is the term used for
the transport of momentum, heat, moisture, vorticity or other atmospheric
properties, by the horizontal movement of air)
The following graph plots the
average mid-latitude vertical pressure gradient and shows how the overall
vertical decrease in pressure – the pressure lapse rate – slows
exponentially as the air becomes less dense with height. In a denser, or colder,
air mass the pressure reduces at a faster rate, conversely in less dense, or
warmer, air the pressure reduces at a slower rate. (The hydrostatic
equation states that the vertical change in pressure, between two levels in
any column of air, is equal to the weight, per unit area, of the air in the
column.) If two air columns have the same pressure change from top to bottom
the denser column will be shorter, conversely if the two columns have the same
height the denser column will have a larger change in pressure from top to
bottom.
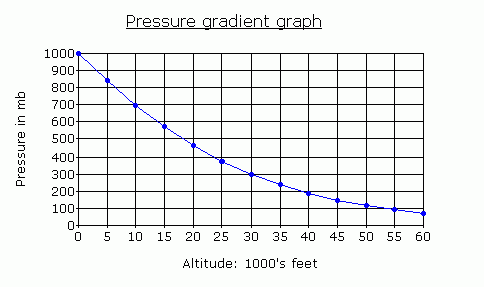
In the ICAO standard atmosphere,
details of which are shown in section 2.1, the rate of altitude change for each
1 hPa change in pressure is approximately:
| zero to 5000 feet: |
30 feet/hPa or 34 hPa per 1000 feet |
| 5000 to 10 000 feet: |
34 feet/hPa or 29 hPa per 1000 feet |
| 10 000 to 20 000 feet: |
43 feet/hPa or 23 hPa per 1000 feet |
| 20 000 to 40 000 feet: |
72 feet/hPa or 14 hPa per 1000 feet |
The change in altitude for one
hectopascal change in pressure can be roughly calculated from the absolute
temperature and the pressure at the level using the equation: = 96T/P feet.
