calculations

Air Speed / Ground Speed

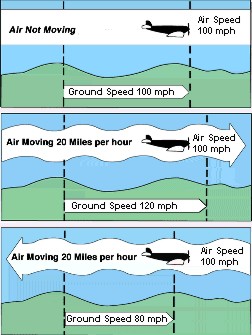
Taking a 60 mile long road trip by car, the driver is fairly sure that if the average speed is 60 miles per hour (mph) for the trip, then it will probably take approximately one hour for the trip (60/60 = 1). This would not be as certain with an airplane because of wind. An airplane's speed can be greatly enhanced or diminished by the wind. This is the reason for the consideration of 2 speeds: ground speed and airspeed. Ground speed is the speed at which an airplane is moving with respect to the ground. Airspeed is the speed of an airplane in relation to the air. (Think of airspeed as the speed at which its propulsion system is set to move it along.) If an airplane is flying with the wind then its ground speed will be enhanced. That means its ground speed will be faster than its airspeed. If an airplane is flying against the wind then its ground speed will be reduced. That means its ground speed will be slower than its airspeed. If an airplane is flying through still air (air with no measurable wind), then its ground speed and airspeed will be the same.

Look at the picture below.

Vectors

The term "vector" is used to describe a course flown by an aircraft. Pilots ask for and air traffic controllers issue a heading or a "vector". A vector quantity represents something that has magnitude and direction. Velocity is an example of a vector quantity. When flying, the pilot needs to know the aircraft's speed and direction. These combine to form a vector that represents velocity. Vectors are represented on a graph using a line segment drawn to scale to show the magnitude (in this case the aircraft's speed). An arrow is placed at the terminal point to indicate the direction of the course. The arrow also differentiates the initial point (starting point) from the opposite end (terminal point). Vectors represented on a graph with the same length and direction are considered to be equal.

Using vector addition you can compute the result of two forces that are applied at the same time to an object. Vector addition is used to solve navigation problems when airplanes fly through moving air. The result of vector addition depends on both the speed and direction of an aircraft's course as well as the wind vector. In the example below, we will consider the effects of the force of an airplane and the force of the wind. Vectors can be represented geometrically using a coordinate system.

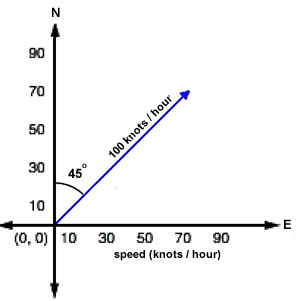
For years, pilots have learned to solve wind correction problems graphically by plotting the vectors using paper, ruler, and protractor. Let's take a look at an example. Imagine an aircraft is flying with a heading of 45 degrees and a speed of 100 knots. A 20-knot wind is blowing due south. What will be the aircraft's groundspeed and course?

We can plot the velocity through the air as a vector with the length of the vector indicating the airspeed and the angle of the vector (measured from north) as the heading.

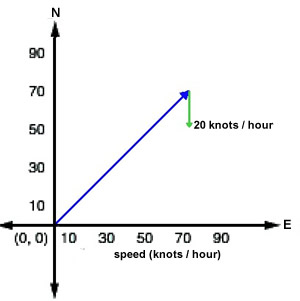
Now imagine that the aircraft is flying through a wind blowing due south at 20 knots. We can plot this as a vector with a length corresponding to 20 knots and pointing straight down. Since we want to add these two vectors together, plot the wind vector so that its tail is at the head of the heading vector.

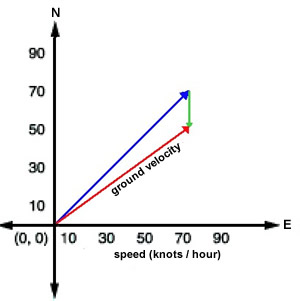
The sum of these two vectors will give the aircraft's direction and speed across the ground. You can simply draw the new vector running from the tail of the heading vector to the head of the wind vector. Its direction can be measured with a protractor, and the speed can be determined by measuring the length of the vector with a ruler. In this case, we measure a groundspeed of about 85 knots and course of about 55 degrees.

If you know some trigonometry, you can quickly and accurately solve this problem without any drawing or measuring. We know that there is a 45-degree angle between our heading and the direction of the wind. We can combine this with the airspeed and windspeed and the law of cosines to find our groundspeed.

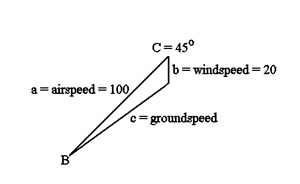
c2 = a2 + b2 - 2ab(cosC)
c2 = 1002 + 202 - 2(100)(20)(cos45)
c = 87

Now that we know our groundspeed, we can use the law of sines to calculate how many degrees we will have to add to our heading to get our course across the ground.
sin B = b (sin C)/ c
sin B = 20 (sin 45)/ 87
B = 9.4 degrees
Adding this angle to our heading gives a course of 54.4 degrees.

Flight Distance

Calculating flight distance on an aeronautical chart is perhaps simpler than planning a driving route on a road map. On the aeronautical chart locate your departure and destination airports. Using a series of straight lines, plot a course from the departure point to the destination point bearing in mind the following:

Flight restrictions for your aircraft (altitude, fuel tank size)
Physical obstructions (such as heights of buildings, towers, mountains, mountain passes)
Other restrictions (such as restricted airspace, restricted airways, assigned airways)


Aeronautical charts usually use as a scale of 1:500,000 (or sometimes written 1/500,000). This means that 1 single unit on the chart (which could be inch, foot, yard, statute mile, nautical mile or kilometre) represents 500,000 of that same unit on the ground. So, if the aeronautical chart uses inches, then 1 inch on the chart equals 500,000 inches on the Earth. Check elsewhere on the chart to see the conversion scale of chart distance to statute or nautical miles. The smaller the scale of the chart, the less the detail can be shown on the chart. With chart measurements being equal, a 1:250,000 scale will provide greater detail than a chart with a scale of a 1:1,000,000 because the first chart will cover a smaller amount of area.

Using the conversion scale as indicated on the aeronautical chart, calculate the total number of miles to be flown by multiplying the total number of inches measured by scale of miles to inches.

Flight Time

Flight time indicates the actual time an aircraft is in the air flying from its departure point to its destination point. The computed flight time is a simple equation of T = D/S or Time equals Distance divided by Speed. Convert the decimal answer to our 60-minutes-to-an-hour and the flight time will be expressed in hours and minutes.

Let's say for example, that a pilot will fly a small Cessna aircraft a distance of 560 miles. The airplane will have an average airspeed of 130 miles per hour moving with the wind which is blowing at 30 mph. How long will the flight take? Take the total number of miles and divide it by the ground speed (airspeed + or - wind speed). The quotient will give the pilot the flight time. Doing the calculation: 560 / (130 + 30) = 560 / 160 = 3.5. Since there are 60 minutes in an hour, the decimal .5 will need to be converted to our 60-minutes-to-an-hour clock.
To do that, take the answer 3.5 and convert as shown below:

3.5 = 3 + (.5 x 60 minutes) = 3 + 30.0 = 3 hours and 30 minutes

What if the pilot in the example above is flying against the wind? Calculating flight time would look like this:

560/ (130 - 30) = 560 / 100 = 5.6

Then convert the answer to minutes:

5.6 = 5 + (.6 x 60 minutes) = 5 + 36.0 = 5 hours and 36 minutes

Fuel Requirements

The pilot of the aircraft makes the decision of how much fuel to carry based upon the following information:

Aircraft operations handbook's specifications for fuel consumption, weight and balance
Payload weight (cargo, baggage and passengers)
Weight of fuel (number of gallons x 6 pounds = total weight of fuel in pounds)
Weather and winds
Total distance of flight
Average flight speed
Number of miles per gallon averaged by the aircraft carrying the weight for this flight

Typically there is a legal minimum fuel limit that all aircraft must follow when determining how much fuel to pump into the tanks. The minimum amount of fuel required needs to be able to fuel the following:

the aircraft from its departure airport to its destination airport
 being able to carry out an approach and go-around
flying to an alternate airport nearby (in case there is weather impediments at the scheduled destination airport)
the ability to fly a 30-minute, holding pattern above the alternate airport land and taxi to the gate

To calculate the amount of fuel needed for a flight, the pilot uses the following equation:

Fuel Flow (gallons per hour) x Time = Fuel Consumed

The pilot uses charts found in the aircraft operation handbook that provides information about the miles per gallon of the aircraft at certain weights. The weight of the fuel is calculated by taking the total number of gallons and multiplying it by 6 pounds. One gallon of fuel weighs 6 pounds. This is usually figured into the charts found in the handbook.

Once the pilot knows the aircraft's fuel consumption rate for the weight being flown and the flight time, the pilot can compute the fuel needed for the flight.

Look at the example below.

8.5 gph (fuel consumption rate) x 1:40 (flight time in hours/minutes) = 14.2 gallons

The pilot of this aircraft will need to make sure that at least 14.5 gallons of fuel are pumped into the fuel tanks for this flight.

Fuel Consumption

How much and how fast an aircraft uses fuel is known as fuel consumption. The same calculation used for determining a car's fuel consumption is also used for an aircraft with additional consideration for the weight of the payload (passengers and/or cargo). All aircraft have an operator's manual that gives specifications such as fuel consumption at different payload weights and fuel amounts. Remember the weight of the fuel also needs to figure into the equation! For example, let's say a small aircraft has a speed range of 120 - 170 mph and holds up to 40 gallons of fuel. Let's say that according to the aircraft's specifications at full payload and fuel weight the aircraft uses 10 gallons of fuel per hour. Take the total amount of fuel (40 gallons) and divide that by the number of gallons used per hour (10) and you will find that the aircraft could be flown for 4 hours. Remember that a good pilot will never fly on fumes, and would stop for re-fuelling long before the 4 hours are up.

Now let's say that the same aircraft is flying with a full tank of fuel, but only half its full payload weight. According to the fuel consumption specifications for this aircraft it will use 8 gallons of fuel per hour. How long will it be able to fly? Do the math: 40 gallons divided by 8 gallons per hour will provide a little over 5 hours of flight time.

True North / Magnetic North

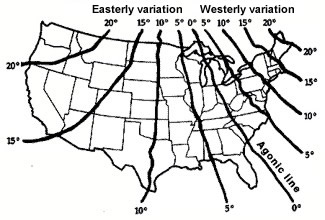
All aeronautical charts are drawn using True North. All airport runways, however, are marked by their magnetic compass directions to the nearest 10°. Runway 5-23 at an airport is a Northeast - Southwest runway. It means if an airplane lands from the SW heading NE on runway 5 the magnetic compass in the airplane would be showing about 050° for the heading. The difference between the magnetic direction and the true direction is called the magnetic variation. All aeronautical charts show the magnetic variation. To convert from a true to magnetic direction many pilots use the saying "East is least, West is best." This serves as a reminder that one subtracts an eastward variation from the true course to get the magnetic course. Inversely, one adds a westward magnetic variation to the true course to get the magnetic course. For example, if the magnetic variation is 15 degrees 30 minutes East, after plotting one's true course, the magnetic course would be the true course minus 15 degrees 5 minutes. Pilots also use the saying "North lags and the south leads." This serves to remind pilots that if he or she turns the airplane from a northerly course the compass first indicates a turn in the opposite direction, then lags behind the actual compass heading. This means that when a pilot rolls out of a turn to a different heading, one must roll out before the compass reads that desired heading. Otherwise the new heading will be a few degrees more than desired (which would eventually lead one way off course). When turning from a southerly heading the compass leads initially, then shows the desired heading before actually reaching that heading.

Another compass error is caused when the airplane is accelerated. The compass indicates a turn to the north. When the airplane decelerates, the compass indicates a turn to the south. From this comes the pilot saying: "Accelerate north, decelerate south." Pilots and air traffic controllers need to be aware of such variations, so as to maintain a proper course at all times.

At many airports the compass variation can be significant. In Anchorage, AK the variation is 25° East while in Dallas, TX the variation is 6° East. However, Nashville, TN the variation is only 1° West.